前端-javascript-基础进阶
Lin
xiaominglin789Javascript 进阶篇
js中的内存空间
二进制运算基础
计算机的存储原理
计算机中的数据分类:
无符号数据-机器码:文件型的数据(0/1)
有符号数据-机器码:符号位 + 数值位 (
0代表正,1代表负)如下:
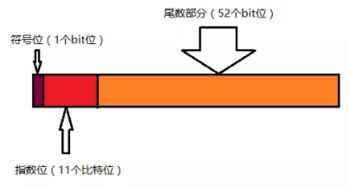
double的二进制:符号位1位 + 指数11位 + 尾数52位- 符号位(sign):第1位是正负数符号位,0代表正数,1代表负数- 指数位(Exponent):中间11位存储指数,用来表示次方数- 尾数位(mantissa):最后的52位是尾数,超出部分自动进一舍零计算机内存储
有符号数据时,存储的都是二进制的补码反码: 为了解决原码做减法的问题补码: 为了 解决了0的符号问题以及0的两个编码问题- 1-1 = 1 + (-1) = [0000 0001]原+ [1000 0001]原= [0000 0001]补+ [1111 1111]补= [1 0000 0000]补=[0000 0000]补=[0000 0000]原 = 0
- 二进制
原码、反码、补码:+ 原码(给人看的):符号位 + 数值位的绝对值+ 反码:+ 正数的反码 = 原码+ 正数的反码 = 除了符号位不变,其他位全部 `0`变`1`, `1`变`0`+ [+1] = [00000001]原 = [00000001]反 = [00000001]补+ 补码(计算和存储的):+ 正数的补码 = 原码 = 反码+ 负数的补码 = 反码 `+1`+ [-1] = [10000001]原 = [11111110]反 = [11111111]补例子(int32): +7 原码: 0b00000000000000000000000000000111 反码: 0b00000000000000000000000000000111 补码: 0b00000000000000000000000000000111
-7原码: 0b10000000000000000000000000000111反码: 0b11111111111111111111111111111000补码: 0b11111111111111111111111111111001
十进制与二进制 - 快速转换:8421码(BCD码):
- 十进制转n进制:十进制 % n,直到商=0,余数反转.
255-以内:
二进制:1 1 1 1 1 1 1 1
十进制:128 64 32 16 8 4 2 1
# 十进制(D) 二进制(B) BCD转换(奇数末位:1,偶数末位:0,再看空位补:0)
1 1 1=1
2 10 2=2+0
3 11 3=2+1
4 100 4=4+0+0
5 101 5=4+0+1
6 110 6=4+2+0
7 111 7=4+2+1
8 1000 8=8+0+0+0
9 1001 9=8+0+0+1
... ...
27 11011 27=16+8+0+2+1
... ...
99 1100010 99=64+32+0+0+0+2+1
100 1100100 100=64+32+0+0+4+0+0
... ...
125 11111101 125=64+32+16+8+4+0+1
按位运算(二进制-用补码运算):
# 按位与:& (同位都为 `1`, 才为 `1`, 否则为 `0`)
3 & 4 = 0 、 107 & 299 = 45 、 -23 & 99 = 97 、-3 & -7 = -7
二进制位: 0 & 0 => 0、 1 & 0 => 0、 0 & 1 => 0、 1 & 1 => 1
# 按位或: | (同位有一个为 `1`, 就为 `1`, 否则为 `0`)
3 | 4 = 7 、 3 | 5 = 7 、-3 | 7 = -1 、-3 | -7 = -3
二进制位: 0 | 0 = 0、 1 | 0 = 1、 0 | 1 = 1、 1 | 1 = 1
# 按位异或:^ (同位值不同: 1, 值同:0)
3 ^ 4 = 7 、 -3 ^ 4 = 7 、 -3 ^ -4 = 1
二进制位: 0 ^ 0 = 0、 1 ^ 0 = 1、 0 ^ 1 = 1、 1 ^ 1 = 0
# 按位取反: ~ (单步运算符,补码所有位:0->1, 1->0)
~2 = -3
二进制位: ~0 = 1、 ~1 = 0
# 左移:<< (放大2^n倍, 操作数 乘以 2的n位次幂)
## 底层原理: 往左移动`n位`,符号位不变,左侧`n位`被挤掉了,右侧空出来的`n位`用`0`补全
3 << 2 = 3*(Math.pow(2, 2)) = 12
=> 3 = 0b00000000000000000000000000000011 (32位)
=> 左移2位,左侧挤掉2位, 0b000000000000000000000000000011 (30位)
=> 右侧补充2位 '0', 0b00000000000000000000000000001100 (32位)
# 右移:>> (缩小2^n倍, 操作数除以 2的n位次幂)
## 底层原理: 往右移动`n位`,右侧挤掉`n位`,左侧空出来的`n位`用`符号位`补满`.
## 正数右移
11 >> 2 = 2; // 11 / (Math.pow(2, 2)) = 2.75 向下取整数: Math.floor()
## 负数右移
-11 >> 2 = -3; // 向下取整数 Math.floor(),js中 Math.floor() 返回的是整数。java中, js中 Math.floor() 返回的是浮整数: -3.0
# 无符号右移:>>>
## 无符号右移。不论正数还是负数,移位过程中高位均补零。
-8 >>> 30 = 1
-11 >>> 30 = 1
-99 >>> 30 = 1
-8 >>> 4 = 268435455
# 不用第三个变量交换2个变量的值
a = 77; b = 99
a = a ^ b
b = a ^ b
a = a ^ b
// a = 99 b = 77